[vc_row][vc_column][vc_empty_space][vc_column_text]
Didática
[/vc_column_text][vc_separator color=”custom” accent_color=”#48184a”][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_single_image image=”5724″ img_size=”full”][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Professores quase Picassos
[/vc_column_text][vc_column_text]
Na hora de estudar e de ensinar, quem desenha os conceitos matemáticos organiza melhor o próprio pensamento. Curiosamente, nem todo estudante recorre logo a desenhos, pois não se julga bom desenhista. Não precisa ser bom — basta tomar uns poucos cuidados
[/vc_column_text][vc_column_text]
Por Aline Viana
[/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Na sala de aula duma grande universidade, a professora dá a seguinte dica aos novatos: “Comprem um dicionário de matemática. Nele, vocês poderão encontrar respostas para grande parte de suas dúvidas.” Um dos estudantes, por precaução, compra dois — ambos em inglês, pois ouviu dizer que são feitos com maior cuidado. Numa das aulas, a professora menciona um nome que ele nunca ouviu falar: toro. Corre para estrear os dicionários. Num deles, mais sucinto, encontra apenas a definição; no outro, vê a definição e também algumas fórmulas. (Pode ver no quadro 1 o verbete mais sucinto.)
Contudo, nenhum dos dois dicionaristas mostra ao leitor uma imagem do toro, que se parece com uma câmara de bicicleta. (Sobre toros, veja o quadro 2.) Talvez, se o estudante tivesse visto a imagem antes, compreenderia melhor o que ele é.
Assim acontece com alguns conceitos difíceis da matemática: quando alguém faz ou vê o desenho, a ideia se torna mais fácil de entender. Alguns professores gostam dessa técnica milenar. Thiago de Melo, professor na Unesp de Rio Claro (SP), diz que, numa sala de aula, é comum o professor desenhar; um desenho faz bem aos alunos e ao professor. “Desenhar nos ajuda a organizar o pensamento.”
Um estudante pode desenhar quase todo conceito matemático, diz Thiago — mesmo conceitos da álgebra, mesmo conceitos avançados. (O próprio Thiago nunca topou com um conceito que não pudesse desenhar, mas usa a palavra “quase” a título de precaução.) Gabriel Ponce, doutor pela USP de São Carlos (SP), diz que, para ele, é automático: tudo o que lê, desenha. No começo, tentava apenas ler; depois percebeu que, quando estudava conceitos complicados sem desenhá-los, logo os esquecia.
O matemático Paul Lockhart, no livro O lamento de um matemático, escreveu: “A matemática é a mais pura das artes, e também a mais mal compreendida.” Alguns estudantes resistem à estratégia de atacar um problema com um desenho; ainda não sabem que já nasceram meio matemáticos, e que, além disso, já nasceram meio artistas também.
Diagrama de Venn ou elipse?
Thiago costuma dar uma dica a seus alunos:
— Vocês podem desenhar um problema para entendê-lo melhor. Mas lembrem-se de que só isso não prova nada.
Ele quer dizer que o desenho é útil, mas é como um mapa. Examinar o mapa para ver como se chega ao topo da montanha não é a mesma coisa que escalar a montanha para valer. “Demonstrar matematicamente é mais importante do que só desenhar”, diz Thiago. “Para quem sabe o que está fazendo, o desenho faz todo sentido. Mas é preciso saber.”
Gabriel Ponce, para escrever a dissertação de mestrado, estudou sistemas dinâmicos. Ele explica: estudava até que ponto certas equações produzem números que qualquer leigo classificaria como “caóticos” ou “imprevisíveis”; para classificar o grau de imprevisibilidade, criou mapas, ou desenhos, com os quais achou mais fácil resolver problemas. “Os sistemas dinâmicos surgiram de problemas da física. Modelos de previsão do tempo, por exemplo, produzem certos estados que podemos chamar de imprevisíveis, porque, antes que produzam os tais estados, é muito difícil prevê-los.”
Os professores também dizem que, com o desenho, o estudante consegue entender melhor conceitos como o de derivada, ou os conceitos da topologia — dos quais o toro é um exemplo. Gabriel, quando estava na faculdade e estudava o conceito de derivada, anotava diligentemente as letras gregas épsilon e delta (e e d). Mas só foi entender o conceito melhor depois de ter feito n desenhos como o da figura 1 — daí ficou óbvio que, se d tende a zero, a inclinação da reta secante à curva da função tende à inclinação da reta tangente. (Se a função for derivável, é claro.) “Ficou muito mais fácil de entender depois que visualizei os desenhos no papel.”[/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
“UM MATEMÁTICO,
COMO UM PINTOR OU
POETA, É UM INVENTOR
DE PADRÕES. SE SEUS
PADRÕES DURAM MAIS
QUE OS DELES, É PORQUE
SÃO FEITOS DE IDEIAS”
Godfrey Harold Hardy (1877-1947),
matemático britânico
[/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text] [/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
[/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
 [/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Thiago, que é pós-doutorado em topologia algébrica, desenha bastante para compreender as ideias mais sofisticadas de sua área. Com um mero desenho, consegue ter uma ideia do grau de dificuldade de um problema. “Por que os desenhos da geometria, da geometria analítica e do cálculo são simples?”, pergunta. “Porque, de modo geral, os conceitos também são simples.” Em situações de pesquisa, diz Thiago, nem sempre é fácil produzir um desenho que ilustre bem um conceito novo. Para quem já estudou conjuntos, um diagrama de Venn faz todo o sentido; para quem nunca estudou, o desenho evoca apenas a ideia de elipses sobrepostas. (Veja a figura 5.) [/vc_column_text][vc_column_text]
[/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Thiago, que é pós-doutorado em topologia algébrica, desenha bastante para compreender as ideias mais sofisticadas de sua área. Com um mero desenho, consegue ter uma ideia do grau de dificuldade de um problema. “Por que os desenhos da geometria, da geometria analítica e do cálculo são simples?”, pergunta. “Porque, de modo geral, os conceitos também são simples.” Em situações de pesquisa, diz Thiago, nem sempre é fácil produzir um desenho que ilustre bem um conceito novo. Para quem já estudou conjuntos, um diagrama de Venn faz todo o sentido; para quem nunca estudou, o desenho evoca apenas a ideia de elipses sobrepostas. (Veja a figura 5.) [/vc_column_text][vc_column_text]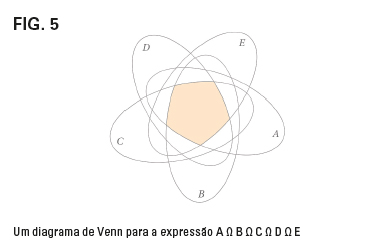 [/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Uma vez, Gabriel se matriculou num curso de topologia na faculdade, e tinha de estudar conceitos como conjunto aberto, conjunto compacto. Eram conceitos que já havia visto, em outro formato, no curso de análise. A professora conseguia desenhá-los de um jeito que Gabriel nem imaginava fosse possível — e só no curso de topologia, vendo os desenhos, entendeu de fato certas ideias do curso de análise. “A definição formal desaparece muito rápido, mas o desenho fica.”
[/vc_column_text][vc_empty_space][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]Uma vez, Gabriel se matriculou num curso de topologia na faculdade, e tinha de estudar conceitos como conjunto aberto, conjunto compacto. Eram conceitos que já havia visto, em outro formato, no curso de análise. A professora conseguia desenhá-los de um jeito que Gabriel nem imaginava fosse possível — e só no curso de topologia, vendo os desenhos, entendeu de fato certas ideias do curso de análise. “A definição formal desaparece muito rápido, mas o desenho fica.”
Agora, quando dá aulas, não se esquece da lição: faz seus alunos desenhem tudo. Chama essa abordagem de “a estratégia do desenho”. “Nosso cérebro”, diz Gabriel, “parece que guarda melhor na memória aquilo que ocupa menos espaço. O estudante que desenha muito guarda mais conceitos que o estudante que só tenta se lembrar de definições abstratas; tenho a impressão de que o desenho ocupa menos espaço. No mundo das ideias, precisamos de imagens para ter boa intuição a respeito dos resultados.”
Como adivinhar resultados
Para uma turma de ensino médio, Thiago sugere que professores desafiem os estudantes com o desenho, e não apenas os mandem desenhar. Quando pede que ataquem um problema, pede também que pensem em como resolvê-lo com desenho e sem desenho — assim se acostumam a atacar problemas que conseguem visualizar (isto é, sobre os quais já têm alguma intuição) e que não conseguem visualizar (sobre os quais ainda não sabem nada). De certa forma, Thiago ensina seus alunos como devem se comportar nas várias fases dos estudos, das fases em que sabem pouco àquelas em que sabem mais.
Gabriel diz que, com o tempo, o estudante melhora sua habilidade de esboçar os conceitos em desenhos; e se o treinamento for bom, ele desconfia do desenho, pois sabe que nenhum desenho representa perfeitamente as fantasias matemáticas. “Quando eu era mais jovem”, diz Gabriel, “copiava as expressões que a professora escrevia na lousa, mas minha cabeça viajava para outros lugares.” É impossível desenhar sem dar atenção ao movimento das mãos. Ao desenhar, portanto, o aluno mantém a mente no lugar e no momento em que a aula transcorre. Esse é o milagre dos desenhos: eles mantêm os alunos atentos.
[/vc_column_text][vc_empty_space][/vc_column][/vc_row]